Manual:HTB

Theory

Structure

Hierarchical Token Bucket (HTB) allows to create hierarchical queue structure and determine relations between parent and child queues and relation between child queues. As soon as queue have at least one child it become a parent queue. All child queues (don't matter how many levels of parents they have) are treated as they were on the same (bottom) level of HTB. Child queues make actual traffic consumption, parent queues are responsible only for traffic distribution. Child queues are not able to get more traffic than parent has.

In RouterOS it is necessary to specify parent option to assign queue as a child to other queue

Dual Limitation

Each queue in HTB have two rate limits:

• CIR (Committed Information Rate) – (limit-at in RouterOS) worst case scenario, flow will get this amount of traffic no matter what (assuming we can actually send so much data)
• MIR (Maximal Information Rate) – (max-limit in RouterOS) best case scenario, rate that flow can get up to, if there is spare bandwidth

In another words, at first HTB will try to satisfy every child queue's limit-at (CIR) only then it will try to reach max-limit (MIR)

To ensure optimal (as designed) usage of dual limitation feature we suggest to stick to these rules:

• Sum of committed rates of all children must be less or equal to amount of traffic that is available to parent.

CIR(parent)* ≥ CIR(child1) +...+ CIR(childN)

*in case if parent is main parent CIR(parent)=MIR(parent)

• Maximal rate of any child must be less or equal to maximal rate of the parent

MIR (parent) ≥ MIR(child1) & MIR (parent) ≥ MIR(child2) & MIR (parent) ≥ MIR(childN)

Priority

Priority is used for creation of the strict order - who will get traffic first. Queue with higher priority will reach its limit-at before the queue with lower priority and after all limit-ats are satisfied queue with higher priority will reach its MIR before the queue with lower priority. 8 is the lowest priority, 1 is the highest.

Make a note that priority only works:

• for child queues - as soon as you assign at least one child to the queue, priority option will have no meaning in this queue
• if limit-at and/or max-limit is specified (not 0)

Example

In this section we will analyze HTB in action. To do so we will take one specific example of HTB in one specific moment in time, when HTB have to recycle specific amount of incoming traffic.

Structure

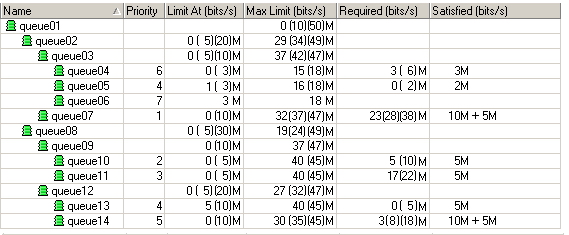
Our HTB structure will consist of 14 queues:

• Queue01 has two childs - Queue02 and Queue08
• Queue02 has two childs - Queue03 and Queue07
• Queue03 has three childs - Queue04, Queue05 and Queue06
• Queue04 child
• Queue05 child
• Queue06 child
• Queue07 child
• Queue08 has two childs - Queue09 and Queue12
• Queue09 has two childs - Queue10 and Queue11
• Queue10 child
• Queue11 child
• Queue12 has two childs - Queue13 and Queue14
• Queue13 child
• Queue14 child

Priorities, limits and amounts of incoming traffic

File:Stage1 1.jpg

Stage 1 - Satisfying the Limit-at

File:Stage1 2.jpg

Stage 2 - Getting closer to Max-limit